Mestre Panda - Prepara-te para os Exames Nacionais

Dificuldade: fácil

Mostrar Enunciado do Grupo

A Figura 1 representa parte de uma montagem utilizada na determinação experimental da capacidade térmica mássica do cobre. Nessa montagem, o sensor de temperatura estava ligado a um sistema de aquisição de dados, e a resistência de aquecimento estava inserida num circuito elétrico.

Na experiência realizada, utilizou-se um bloco calorimétrico de cobre de massa $1,264 \mathrm{~kg}$. Além das grandezas elétricas, mediu-se a temperatura do bloco, ao longo do processo de aquecimento.

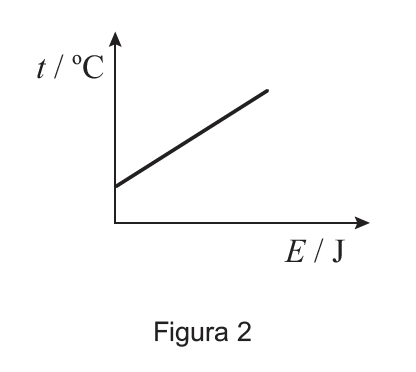
Com os valores obtidos, foi possível traçar o gráfico da temperatura, $t$, do bloco de cobre em função da energia, $E$, que the foi fornecida, cujo esboço se representa na Figura 2. Determinou-se, seguidamente, a equação da reta que melhor se ajustava ao conjunto de pontos desse gráfico:

$$t=1,91 \times 10^{-3} E+22,1$$

Questão:

Determine o erro percentual (erro relativo, em percentagem) da capacidade térmica mássica do cobre obtida nesta experiência, tomando como referência o valor tabelado $385 \mathrm{~J} \mathrm{~kg}^{-1}{ }^{\circ} \mathrm{C}^{-1}$.

Apresente todas as etapas de resolução.

Fonte: Exame - 2017, Época especial

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Questão:

Escreve a tua resposta aqui:

Comentários