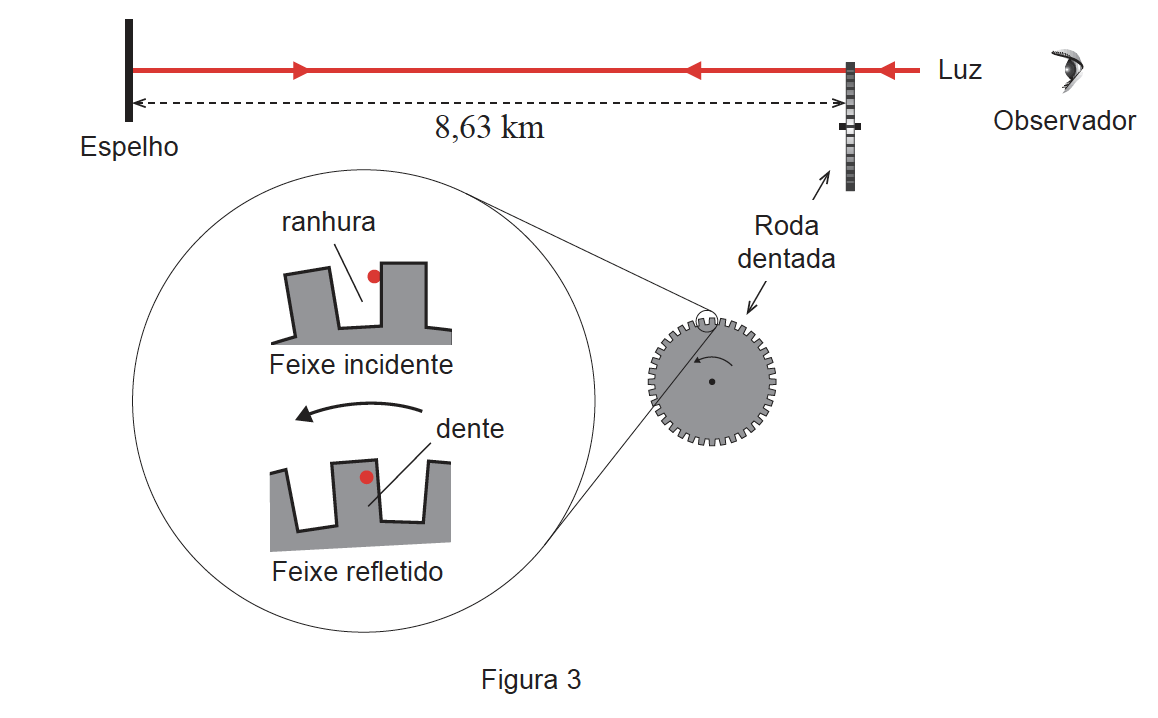
Em 1849, Hippolyte Fizeau mediu a velocidade da luz no ar com base na experiência esquematizada na Figura 3 (que não está à escala). Nessa experiência, um feixe de luz passava numa ranhura, na periferia de uma roda dentada, e era, a seguir, refletido num espelho colocado a uma distância de $8,63 \mathrm{~km}$ da roda.
Com a roda parada, o feixe refletido no espelho voltava a passar na mesma ranhura.
Com a roda a girar com uma frequência de $12,6 \mathrm{~Hz}$, o feixe refletido no espelho não voltava a passar pela ranhura, incidindo no dente imediatamente a seguir, deixando de ser detetado pelo observador. Nestas condições, a roda descrevia um ângulo de $0,250^{\circ}$ desde o instante em que o feixe incidente passava pela ranhura até ao instante em que o feixe refletido incidia no dente.
Questão:
Determine a velocidade da luz no ar, tal como é obtida a partir da experiência descrita.
Apresente todos os cálculos efetuados.
Fonte: IAVE
Fonte: IAVE
Resolução do Exercício:
1) Calcula o intervalo de tempo desde a passagem da luz pela ranhura até incidir no dente imediatamente a seguir da roda.
$$\frac{1 \mathrm{~s}}{12,6 \text { voltas }}=\frac{T}{1 \text { volta }} \Leftrightarrow T=7,934 \times 10^{-2} \mathrm{~s}$$
Assim, vem que $$\frac{360^{\circ}}{7,934 \times 10^{-2} \mathrm{~s}}=\frac{0,250^{\circ}}{t} \Leftrightarrow t=5,512 \times 10^{-5} \mathrm{~s}$$
OU
$$\begin{aligned}\frac{1 \mathrm{~s}}{12,6 \text { voltas }}=\frac{T}{1 \text { volta }} \Leftrightarrow T=7,934 \times 10^{-2} \mathrm{~s}\\\\\omega=\frac{2 \pi}{T} \Leftrightarrow \omega=\frac{360^{\circ}}{7,934 \times 10^{-2} \mathrm{~s}}=4,537 \times 10^{3~\circ}\mathrm{s}^{-1}\\\\\frac{4,537 \times 10^{3 \mathrm{o}}}{1 \mathrm{~s}}=\frac{0,250^{\circ}}{t} \Leftrightarrow t=5,510 \times 10^{-5} \mathrm{~s}\end{aligned}$$
2) Calcula a velocidade da luz no ar, obtida a partir da experiência descrita.
$$v=\frac{\Delta d}{\Delta t} \Leftrightarrow v=\frac{2 \times 8,63 \times 10^{3} \mathrm{~m}}{5,512 \times 10^{-5} \mathrm{~s}}=3,13 \times 10^{8} \mathrm{~m} \mathrm{~s}^{-1}$$
Fonte: Lucas Campos
Assinala os critérios que a tua resposta incluiu corretamente:
Comentários
Para responder ao comentário, por favor inicia sessão ou cria uma conta.
Multiplica-se por dois porque o feixe de luz percorre duas vezes a distância: vai até ao espelho e volta porque é refletida.
Para responder ao comentário, por favor inicia sessão ou cria uma conta.
Para comentar, por favor inicia sessão ou cria uma conta.