Mestre Panda - Prepara-te para os Exames Nacionais

Dificuldade: fácil

Mostrar Enunciado do Grupo

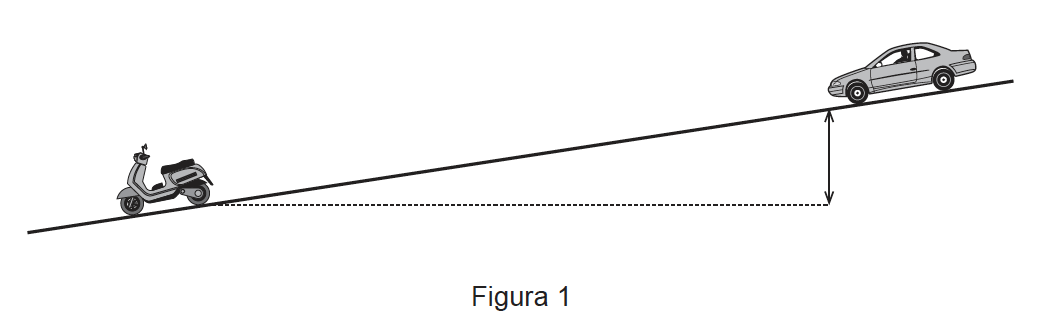
Um automóvel encontrava-se estacionado no cimo de uma rampa, como se representa na Figura 1 (que não está à escala), quando, acidentalmente, se destravou. Deslizou ao longo da rampa, com aceleração constante, até colidir com um motociclo que se encontrava parado.

Considere que, no movimento considerado, a resultante das forças dissipativas que atuaram no automóvel não foi desprezável, e considere que o automóvel pode ser representado pelo seu centro de massa (modelo da partícula material).

O automóvel, de massa $1,2 \times 10^{3} \mathrm{~kg}$, deslizou $80 \mathrm{~m}$ ao longo da rampa até colidir com o motociclo. A análise do acidente permitiu determinar que o módulo da velocidade do automóvel no instante da colisão era $7,5 \mathrm{~m} \mathrm{~s}^{-1}$.

Considere que o desnível entre as posições inicial e final do automóvel era 7,0 m.

Questão:

Determine, a partir de considerações energéticas, a intensidade da resultante das forças dissipativas que atuaram no automóvel paralelamente ao deslocamento.

Explicite o seu raciocínio, indicando todos os cálculos efetuados.

Fonte: Exame - 2020, 2ª fase

Resumos

Exercício Anterior

Próximo Exercício

Comentários

josebel jeremias

Criado em 25/06/2025 11:33

como é que sabemos que o cos é 180?

Responder |

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

Beatriz Silva

Criado em 10/07/2025 07:50

Como é uma força dissipativa o cos tem que ser superior a 90 (realiza trabalho resistente) e como é a única tem que ser máxima, isto é, tem a mesma direção, mas sentido contrário (pq é dissipativa, resistente) ao descolamento. Por isso, dizemos que ela realiza um trabalho máximo resistente de cos 180 ( que é -1, o máximo negativo do cos)

Responder |

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Questão:

Escreve a tua resposta aqui:

Comentários