Mestre Panda

Dificuldade: fácil

Mostrar Enunciado do Grupo

Uma das opções de mobilidade sustentável nas cidades passa pelo uso da bicicleta como meio de transporte.

Na Figura 3, que não está à escala, está representada uma ciclista que se desloca numa trajetória retilínea, numa ciclovia. A ciclovia tem um troço horizontal, entre A e B, e um troço de inclinação constante, entre B e C.

O conjunto, de massa $m$, constituído pela ciclista e pela sua bicicleta não motorizada pode ser representado pelo seu centro de massa (modelo da partícula material).

Questão:

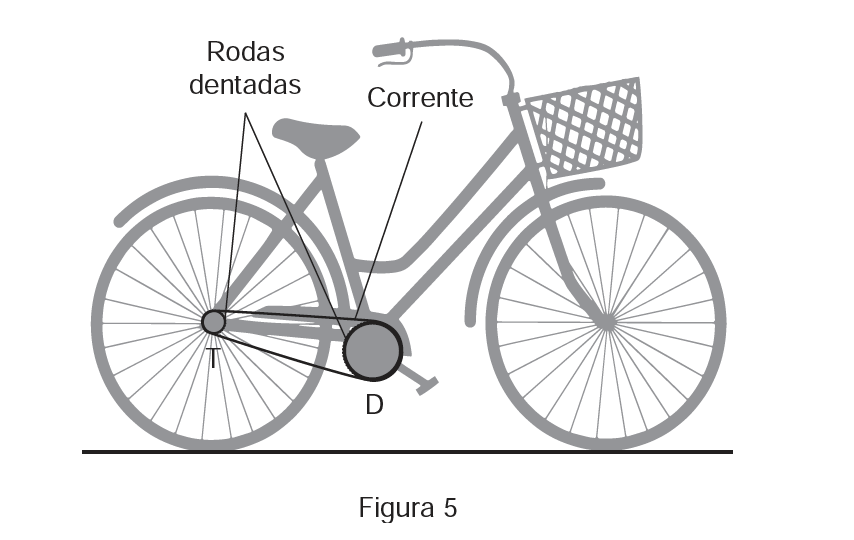
As bicicletas têm uma corrente que liga uma roda dentada dianteira, $D$, movimentada pelos pedais, a uma roda dentada traseira, $\mathrm{T}$, fixa à roda traseira, tal como se representa na Figura 5.

Considere uma rotação completa da roda dentada dianteira, D, em $1 \mathrm{~s}$.

Mostre que, quanto maior for a razão dos raios das duas rodas dentadas, $\frac{r_{\mathrm{D}}}{r_{\mathrm{T}}}$, maior será a frequência de rotação da roda dentada traseira, $T$.

Comece por relacionar as velocidades lineares das rodas dentadas D e T.

Fonte: Exame Física e Química A - 2022, Época Especial - Grupo 4 Exercício 4.3

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Neste momento, não há comentários para este exercício.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Questão:

Escreve a tua resposta aqui:

Comentários