Mestre Panda - Prepara-te para os Exames Nacionais

Dificuldade: fácil

Mostrar Enunciado do Grupo

Um carrinho telecomandado, de massa $400 \mathrm{~g}$, move-se numa pista retilínea, coincidente com um referencial unidimensional, $\mathrm{O} x$.

Admita que o carrinho pode ser representado pelo seu centro de massa (modelo da partícula material).

Na Figura 1, encontra-se representado o gráfico da componente escalar da velocidade, $v_{X}$, desse carrinho, segundo o referencial $\mathrm{O} x$ considerado, em função do tempo, $t$.

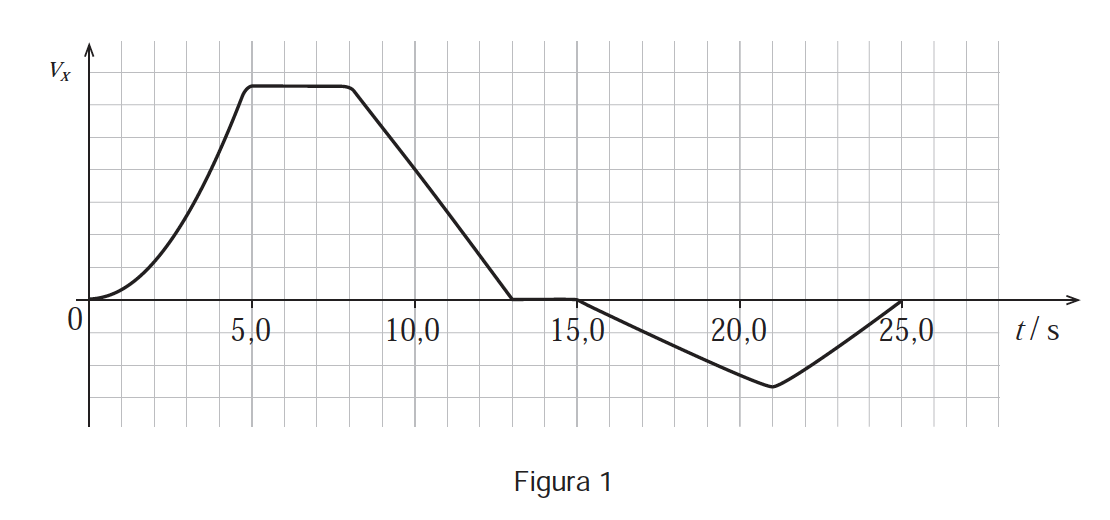
Questão:

No intervalo de tempo $[8,0 ; 13,0] \mathrm{s}$, o carrinho percorreu $3,2 \mathrm{~m}$.

Calcule, sem recorrer a conceitos energéticos, a intensidade da resultante das forças que atuam no carrinho, nesse intervalo de tempo.

Apresente todas as etapas de resolução.

Fonte: Exame - 2018, Época especial

Resumos

Exercício Anterior

Próximo Exercício

Comentários

Adriana Rafaela Sousa

Criado em 24/06/2025 11:52

não entendi

Responder |

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

Mestre Panda Adriana Rafaela Sousa

Criado em 24/06/2025 13:19

Simplificámos a resolução! Diz se ficaste com dúvidas!

Responder |

Para responder ao comentário, por favor inicia sessão ou cria uma conta.

Para comentar, por favor inicia sessão ou cria uma conta.

Selecionar Exercício

Questão:

Escreve a tua resposta aqui:

Comentários