Questão:
Para o estudo das características de um movimento circular uniforme, realizaram-se, em contexto real, num carrossel, medições do módulo da aceleração em função do raio, utilizando sensores de aceleração em telemóveis (smartphones).
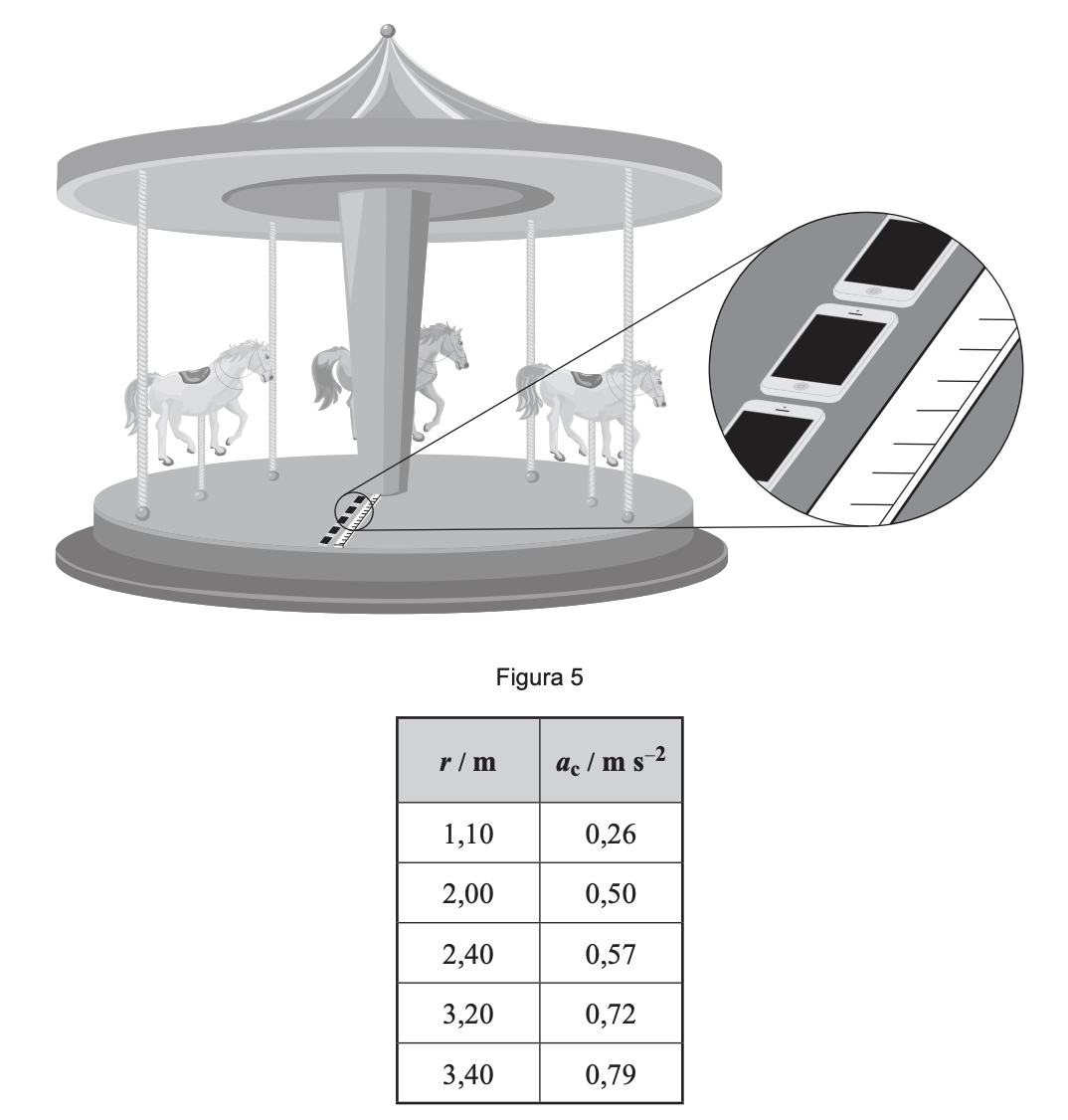
Tal como é ilustrado na Figura 5, num carrossel circular, fixaram-se cinco telemóveis em posições diferentes, numa direção radial.
Na tabela seguinte, estão registados os raios, $r$, e os módulos da aceleração centrípeta, $a_{\mathrm{c}}$, medidos.
Determine o módulo da velocidade angular, nas condições em que decorre a experiência, a partir da equação da reta de ajuste a um gráfico adequado.
Na sua resposta:
– identifique as variáveis independente e dependente a considerar nos eixos do gráfico;
– apresente a equação da reta de ajuste ao gráfico;
– apresente o valor solicitado com dois algarismos significativos.
Apresente todos os cálculos efetuados.
Fonte: IAVE
Fonte: IAVE
Resolução do Exercício:
Atendendo à fórmula para o cálculo da aceleração centrípeta:
$$a_{\mathrm{c}}=\frac{v^{2}}{r}\Leftrightarrow a_{\mathrm{c}}=\frac{(\omega \times r)^{2}}{r}\Leftrightarrow a_{\mathrm{c}}=\frac{\omega^{2} \times r^{2}}{r}\Leftrightarrow a_{\mathrm{c}}=\omega^{2} \times r$$
A bateria de dados na tabela pode ser inserida na calculadora, de modo a obter a reta de mínimos quadrados da função $F(r)=\omega^{2} \times r$, na qual $r$ (a distância do telemóvel ao centro do carrossel) é a variável independente, $\omega^{2}$ (o quadrado da velocidade angular) é o declive e $a_{\mathrm{c}}$ (a aceleração centrípeta do carrossel) a variável dependente.
Daqui é possível obter a reta de mínimos quadrados, com a seguinte equação:
$$
y=0,221 a+0,033
$$
Sendo $\omega^{2}$ sensivelmente igual ao valor do declive apresentado:
$$
\omega^{2}=0,221\Leftrightarrow \omega=\sqrt{0,221}\Leftrightarrow \omega \approx 0,47 \mathrm{~rad} \mathrm{~s}^{-1}
$$
Resposta: 0 módulo da velocidade angular é de $0,47 \mathrm{~rad} \mathrm{s}^{-1}$.
Fonte: Mestre Panda
Assinala os critérios que a tua resposta incluiu corretamente:
Comentários
Para responder ao comentário, por favor inicia sessão ou cria uma conta.
Para responder ao comentário, por favor inicia sessão ou cria uma conta.
Para comentar, por favor inicia sessão ou cria uma conta.