Cria conta para teres acesso a vídeos, estatísticas do teu progresso, exercícios originais e mais!
Selecionar Exercício
Escolhe de entre os grupos: Errados, Novos e Certos
#670 - Exame Física e Química A - 2014, 1ª Fase
Energia, fenómenos térmicos e radiação
#711 - Exame Física e Química A - 2017, 1ª Fase
Forças e movimentos
#793 - Exame Física e Química A - 2014, 1ª Fase
Ondas eletromagnéticas
#718 - Exame Física e Química A - 2017, 1ª Fase
Sinais e ondas
#698 - Exame Física e Química A - 2017, 1ª Fase
Energia, fenómenos térmicos e radiação
#10.1 - Exame Física e Química A - 2023, 2ª Fase
Energia, fenómenos térmicos e radiação
#442 - Exame Física e Química A - 2018, 1ª Fase
Sinais e ondas
#316 - Exame Física e Química A - 2019, 1ª Fase
Tempo, posição, velocidade e aceleração
#5.2.2 - Exame Física e Química A - 2023, 1ª Fase
Forças e movimentos
#463 - Exame Física e Química A - 2017, 1ª Fase
Energia, fenómenos térmicos e radiação
#2.1 - Exame Física e Química A - 2024, 2ª Fase
Interações e seus efeitos
#218 - Exame Física e Química A - 2020, 1ª Fase
Energia e movimentos
#435 - Exame Física e Química A - 2018, 1ª Fase
Energia e movimentos
#3.3 - Exame Física e Química A - 2024, 2ª Fase
Energia, fenómenos térmicos e radiação
#2.1 - Exame Física e Química A - 2022, 2ª Fase
Energia e movimentos
#4.2.3 - Exame Física e Química A - 2022, Época Especial
Energia e movimentos
#10.2 - Exame Física e Química A - 2021, 1ª Fase
Sinais e ondas
#498 - Exame Física e Química A - 2017, 1ª Fase
Ondas eletromagnéticas
#406 - Exame Física e Química A - 2018, 1ª Fase
Energia e movimentos
#3.2 - Exame Física e Química A - 2024, 1ª Fase
Tempo, posição, velocidade e aceleração
#6.2 - Exame Física e Química A - 2024, 1ª Fase
Energia e fenómenos elétricos
#441 - Exame Física e Química A - 2018, 1ª Fase
Sinais e ondas
#674 - Exame Física e Química A - 2014, 1ª Fase
Ondas eletromagnéticas
#9.1 - Exame Física e Química A - 2021, 1ª Fase
Tempo, posição, velocidade e aceleração
#497 - Exame Física e Química A - 2017, 1ª Fase
Energia, fenómenos térmicos e radiação
#279 - Exame Física e Química A - 2020, 1ª Fase
Eletromagnetismo
#6.1 - Exame Física e Química A - 2022, 2ª Fase
Tempo, posição, velocidade e aceleração
#430 - Exame Física e Química A - 2018, 1ª Fase
Tempo, posição, velocidade e aceleração
#7.2 - Exame Física e Química A - 2024, 1ª Fase
Energia e movimentos
#7.1 - Exame Física e Química A - 2024, Época Especial
Forças e movimentos
#433 - Exame Física e Química A - 2018, 1ª Fase
Energia e movimentos
#695 - Exame Física e Química A - 2017, 1ª Fase
Energia e fenómenos elétricos
#467 - Exame Física e Química A - 2017, 1ª Fase
Sinais e ondas
#1.2 - Exame Física e Química A - 2021, 1ª Fase
Energia e movimentos
#278 - Exame Física e Química A - 2020, 1ª Fase
Eletromagnetismo
#527 - Exame Física e Química A - 2016, 1ª Fase
Energia, fenómenos térmicos e radiação
#315 - Exame Física e Química A - 2019, 1ª Fase
Interações e seus efeitos
#733 - Exame Física e Química A - 2016, 1ª Fase
Ondas eletromagnéticas
#9.2.1 - Exame Física e Química A - 2023, Época Especial
Forças e movimentos
#468 - Exame Física e Química A - 2017, 1ª Fase
Sinais e ondas
#6.1 - Exame Física e Química A - 2024, Época Especial
Energia e fenómenos elétricos
#5.2 - Exame Física e Química A - 2021, 2ª Fase
Ondas eletromagnéticas
#336 - Exame Física e Química A - 2019, 1ª Fase
Eletromagnetismo
#339 - Exame Física e Química A - 2019, 1ª Fase
Ondas eletromagnéticas
#301 - Exame Física e Química A - 2019, 1ª Fase
Energia, fenómenos térmicos e radiação
#6.2 - Exame Física e Química A - 2022, 2ª Fase
Tempo, posição, velocidade e aceleração
#2.1 - Exame Física e Química A - 2023, 1ª Fase
Sinais e ondas
#753 - Exame Física e Química A - 2015, 1ª Fase
Ondas eletromagnéticas
#384 - Exame Física e Química A - 2018, 1ª Fase
Sinais e ondas
#382 - Exame Física e Química A - 2018, 1ª Fase
Forças e movimentos
#217 - Exame Física e Química A - 2020, 1ª Fase
Interações e seus efeitos
#1.1.3 - Exame Física e Química A - 2022, 1ª Fase
Interações e seus efeitos
#1.3.1 - Exame Física e Química A - 2022, 2ª Fase
Forças e movimentos
#9 - Exame Física e Química A - 2023, 1ª Fase
Forças e movimentos
#3.2 - Exame Física e Química A - 2023, 2ª Fase
Ondas eletromagnéticas
#575 - Exame Física e Química A - 2015, 1ª Fase
Energia, fenómenos térmicos e radiação
#345 - Exame Física e Química A - 2019, 1ª Fase
Interações e seus efeitos
#528 - Exame Física e Química A - 2016, 1ª Fase
Energia, fenómenos térmicos e radiação
#4.2 - Exame Física e Química A - 2022, 2ª Fase
Energia e fenómenos elétricos
#529 - Exame Física e Química A - 2016, 1ª Fase
Energia, fenómenos térmicos e radiação
#6.2 - Exame Física e Química A - 2023, Época Especial
Energia e movimentos
#5.1 - Exame Física e Química A - 2023, Época Especial
Tempo, posição, velocidade e aceleração
#7.1 - Exame Física e Química A - 2021, 2ª Fase
Energia e fenómenos elétricos
#376 - Exame Física e Química A - 2018, 1ª Fase
Energia, fenómenos térmicos e radiação
#796 - Exame Física e Química A - 2014, 1ª Fase
Energia e movimentos
#6.1 - Exame Física e Química A - 2023, Época Especial
Forças e movimentos
#629 - Exame Física e Química A - 2015, 1ª Fase
Forças e movimentos
#5.5 - Exame Física e Química A - 2023, 1ª Fase
Energia e movimentos
#3.1 - Exame Física e Química A - 2024, 1ª Fase
Forças e movimentos
#632 - Exame Física e Química A - 2014, 1ª Fase
Eletromagnetismo
#8.1 - Exame Física e Química A - 2023, 2ª Fase
Eletromagnetismo
#5.2 - Exame Física e Química A - 2021, Época Especial
Forças e movimentos
#9.2 - Exame Física e Química A - 2021, 1ª Fase
Interações e seus efeitos
#1.1 - Exame Física e Química A - 2024, 2ª Fase
Sinais e ondas
#6.2 - Exame Física e Química A - 2022, 1ª Fase
Sinais e ondas
#521 - Exame Física e Química A - 2016, 1ª Fase
Sinais e ondas
#4 - Exame Física e Química A - 2021, Época Especial
Sinais e ondas
#487 - Exame Física e Química A - 2017, 1ª Fase
Energia e movimentos
#3.2 - Exame Física e Química A - 2021, 1ª Fase
Forças e movimentos
#7.2 - Exame Física e Química A - 2021, 2ª Fase
Energia e fenómenos elétricos
#4.2 - Exame Física e Química A - 2024, Época Especial
Ondas eletromagnéticas
#9.3 - Exame Física e Química A - 2021, 1ª Fase
Energia e movimentos
#500 - Exame Física e Química A - 2017, 1ª Fase
Ondas eletromagnéticas
#2.1 - Exame Física e Química A - 2021, 2ª Fase
Forças e movimentos
#434 - Exame Física e Química A - 2018, 1ª Fase
Energia e movimentos
#436 - Exame Física e Química A - 2018, 1ª Fase
Energia e movimentos
#431 - Exame Física e Química A - 2018, 1ª Fase
Interações e seus efeitos
#7.3 - Exame Física e Química A - 2024, Época Especial
Tempo, posição, velocidade e aceleração
#518 - Exame Física e Química A - 2016, 1ª Fase
Tempo, posição, velocidade e aceleração
#671 - Exame Física e Química A - 2014, 1ª Fase
Energia, fenómenos térmicos e radiação
#7 - Exame Física e Química A - 2023, Época Especial
Eletromagnetismo
#9.1 - Exame Física e Química A - 2023, Época Especial
Energia e movimentos
#2.2.2 - Exame Física e Química A - 2023, Época Especial
Energia, fenómenos térmicos e radiação
#716 - Exame Física e Química A - 2017, 1ª Fase
Eletromagnetismo
#710 - Exame Física e Química A - 2017, 1ª Fase
Forças e movimentos
#606 - Exame Física e Química A - 2015, 1ª Fase
Ondas eletromagnéticas
#224 - Exame Física e Química A - 2020, 1ª Fase
Forças e movimentos
#229 - Exame Física e Química A - 2020, 1ª Fase
Eletromagnetismo
#231 - Exame Física e Química A - 2020, 1ª Fase
Energia e fenómenos elétricos
#228 - Exame Física e Química A - 2020, 1ª Fase
Eletromagnetismo
#225 - Exame Física e Química A - 2020, 1ª Fase
Energia e movimentos
#792 - Exame Física e Química A - 2014, 1ª Fase
Ondas eletromagnéticas
#4 - Exame Física e Química A - 2021, 1ª Fase
Ondas eletromagnéticas
#3.1 - Exame Física e Química A - 2021, 1ª Fase
Ondas eletromagnéticas
#10.1 - Exame Física e Química A - 2021, 1ª Fase
Sinais e ondas
#2.2 - Exame Física e Química A - 2021, 1ª Fase
Energia e fenómenos elétricos
#276 - Exame Física e Química A - 2020, 1ª Fase
Energia, fenómenos térmicos e radiação
#717 - Exame Física e Química A - 2017, 1ª Fase
Sinais e ondas
#281 - Exame Física e Química A - 2020, 1ª Fase
Energia e fenómenos elétricos
#299 - Exame Física e Química A - 2019, 1ª Fase
Energia e fenómenos elétricos
#320 - Exame Física e Química A - 2019, 1ª Fase
Energia e movimentos
#298 - Exame Física e Química A - 2019, 1ª Fase
Energia, fenómenos térmicos e radiação
#494 - Exame Física e Química A - 2017, 1ª Fase
Energia, fenómenos térmicos e radiação
#2.2.1 - Exame Física e Química A - 2023, Época Especial
Energia e fenómenos elétricos
#697 - Exame Física e Química A - 2017, 1ª Fase
Energia, fenómenos térmicos e radiação
#262 - Exame Física e Química A - 2020, 1ª Fase
Forças e movimentos
#4.2.1 - Exame Física e Química A - 2022, Época Especial
Energia e movimentos
#2.2 - Exame Física e Química A - 2022, Época Especial
Energia, fenómenos térmicos e radiação
#4.2.2 - Exame Física e Química A - 2022, Época Especial
Interações e seus efeitos
#576 - Exame Física e Química A - 2015, 1ª Fase
Energia, fenómenos térmicos e radiação
#638 - Exame Física e Química A - 2014, 1ª Fase
Energia, fenómenos térmicos e radiação
#639 - Exame Física e Química A - 2014, 1ª Fase
Energia e movimentos
#9.2 - Exame Física e Química A - 2024, Época Especial
Energia, fenómenos térmicos e radiação
#2.2.2 - Exame Física e Química A - 2021, 2ª Fase
Energia, fenómenos térmicos e radiação
#4.2 - Exame Física e Química A - 2021, 2ª Fase
Forças e movimentos
#4.1 - Exame Física e Química A - 2021, 2ª Fase
Forças e movimentos
#6.1 - Exame Física e Química A - 2021, 2ª Fase
Energia e movimentos
#344 - Exame Física e Química A - 2019, 1ª Fase
Interações e seus efeitos
#343 - Exame Física e Química A - 2019, 1ª Fase
Energia e movimentos
#333 - Exame Física e Química A - 2019, 1ª Fase
Energia, fenómenos térmicos e radiação
#6.2 - Exame Física e Química A - 2021, Época Especial
Ondas eletromagnéticas
#2.3 - Exame Física e Química A - 2021, Época Especial
Forças e movimentos
#6.1 - Exame Física e Química A - 2021, Época Especial
Ondas eletromagnéticas
#7.2 - Exame Física e Química A - 2021, Época Especial
Energia e fenómenos elétricos
#641 - Exame Física e Química A - 2014, 1ª Fase
Energia e movimentos
#4.2 - Exame Física e Química A - 2024, 2ª Fase
Tempo, posição, velocidade e aceleração
#3.2 - Exame Física e Química A - 2024, 2ª Fase
Energia e fenómenos elétricos
#4.1 - Exame Física e Química A - 2024, 2ª Fase
Energia e movimentos
#9.1 - Exame Física e Química A - 2024, Época Especial
Forças e movimentos
#555 - Exame Física e Química A - 2016, 1ª Fase
Energia, fenómenos térmicos e radiação
#5.3 - Exame Física e Química A - 2023, 1ª Fase
Ondas eletromagnéticas
#4.1 - Exame Física e Química A - 2022, 2ª Fase
Energia, fenómenos térmicos e radiação
#8.2 - Exame Física e Química A - 2022, 2ª Fase
Ondas eletromagnéticas
#1.3 - Exame Física e Química A - 2022, 1ª Fase
Forças e movimentos
#727 - Exame Física e Química A - 2016, 1ª Fase
Energia e movimentos
#721 - Exame Física e Química A - 2016, 1ª Fase
Forças e movimentos
#477 - Exame Física e Química A - 2017, 1ª Fase
Interações e seus efeitos
#368 - Exame Física e Química A - 2019, 1ª Fase
Energia, fenómenos térmicos e radiação
#355 - Exame Física e Química A - 2019, 1ª Fase
Forças e movimentos
#517 - Exame Física e Química A - 2016, 1ª Fase
Forças e movimentos
#489 - Exame Física e Química A - 2017, 1ª Fase
Tempo, posição, velocidade e aceleração
#5.2 - Exame Física e Química A - 2022, 1ª Fase
Energia, fenómenos térmicos e radiação
#490 - Exame Física e Química A - 2017, 1ª Fase
Energia e movimentos
#275 - Exame Física e Química A - 2020, 1ª Fase
Energia e movimentos
#624 - Exame Física e Química A - 2015, 1ª Fase
Energia, fenómenos térmicos e radiação
#472 - Exame Física e Química A - 2017, 1ª Fase
Energia e movimentos
#480 - Exame Física e Química A - 2017, 1ª Fase
Interações e seus efeitos
#386 - Exame Física e Química A - 2018, 1ª Fase
Ondas eletromagnéticas
#8 - Exame Física e Química A - 2023, 1ª Fase
Energia, fenómenos térmicos e radiação
#669 - Exame Física e Química A - 2014, 1ª Fase
Energia, fenómenos térmicos e radiação
#8.2 - Exame Física e Química A - 2024, 1ª Fase
Sinais e ondas
#627 - Exame Física e Química A - 2015, 1ª Fase
Energia e movimentos
#553 - Exame Física e Química A - 2016, 1ª Fase
Energia, fenómenos térmicos e radiação
#351 - Exame Física e Química A - 2019, 1ª Fase
Energia, fenómenos térmicos e radiação
#719 - Exame Física e Química A - 2017, 1ª Fase
Sinais e ondas
#2.1 - Exame Física e Química A - 2021, 1ª Fase
Energia e fenómenos elétricos
#255 - Exame Física e Química A - 2020, 1ª Fase
Tempo, posição, velocidade e aceleração
#640 - Exame Física e Química A - 2014, 1ª Fase
Energia e movimentos
#342 - Exame Física e Química A - 2019, 1ª Fase
Energia e movimentos
#7.2 - Exame Física e Química A - 2022, 1ª Fase
Energia e fenómenos elétricos
#729 - Exame Física e Química A - 2016, 1ª Fase
Energia, fenómenos térmicos e radiação
#352 - Exame Física e Química A - 2019, 1ª Fase
Energia e movimentos
#520 - Exame Física e Química A - 2016, 1ª Fase
Forças e movimentos
#338 - Exame Física e Química A - 2019, 1ª Fase
Ondas eletromagnéticas
#673 - Exame Física e Química A - 2014, 1ª Fase
Ondas eletromagnéticas
#341 - Exame Física e Química A - 2019, 1ª Fase
Forças e movimentos
#662 - Exame Física e Química A - 2014, 1ª Fase
Energia e movimentos
#2.1 - Exame Física e Química A - 2023, Época Especial
Energia, fenómenos térmicos e radiação
#714 - Exame Física e Química A - 2017, 1ª Fase
Energia e movimentos
#4.2.4 - Exame Física e Química A - 2022, Época Especial
Eletromagnetismo
#6.3 - Exame Física e Química A - 2021, 2ª Fase
Interações e seus efeitos
#223 - Exame Física e Química A - 2020, 1ª Fase
Forças e movimentos
#712 - Exame Física e Química A - 2017, 1ª Fase
Energia e movimentos
#8.1 - Exame Física e Química A - 2022, 2ª Fase
Ondas eletromagnéticas
#586 - Exame Física e Química A - 2015, 1ª Fase
Sinais e ondas
#552 - Exame Física e Química A - 2016, 1ª Fase
Energia, fenómenos térmicos e radiação
#581 - Exame Física e Química A - 2015, 1ª Fase
Forças e movimentos
#8.1 - Exame Física e Química A - 2024, 1ª Fase
Sinais e ondas
#1.1.2 - Exame Física e Química A - 2022, 1ª Fase
Energia e movimentos
#630 - Exame Física e Química A - 2015, 1ª Fase
Forças e movimentos
#432 - Exame Física e Química A - 2018, 1ª Fase
Interações e seus efeitos
#3 - Exame Física e Química A - 2023, Época Especial
Ondas eletromagnéticas
#318 - Exame Física e Química A - 2019, 1ª Fase
Energia e movimentos
#332 - Exame Física e Química A - 2019, 1ª Fase
Energia e fenómenos elétricos
#2.2 - Exame Física e Química A - 2024, 2ª Fase
Forças e movimentos
#798 - Exame Física e Química A - 2014, 1ª Fase
Forças e movimentos
#636 - Exame Física e Química A - 2014, 1ª Fase
Energia, fenómenos térmicos e radiação
#2.2.1 - Exame Física e Química A - 2021, 2ª Fase
Energia, fenómenos térmicos e radiação
#383 - Exame Física e Química A - 2018, 1ª Fase
Sinais e ondas
#582 - Exame Física e Química A - 2015, 1ª Fase
Energia e movimentos
#580 - Exame Física e Química A - 2015, 1ª Fase
Forças e movimentos
#478 - Exame Física e Química A - 2017, 1ª Fase
Interações e seus efeitos
#402 - Exame Física e Química A - 2018, 1ª Fase
Forças e movimentos
#642 - Exame Física e Química A - 2014, 1ª Fase
Interações e seus efeitos
#574 - Exame Física e Química A - 2015, 1ª Fase
Energia, fenómenos térmicos e radiação
#699 - Exame Física e Química A - 2017, 1ª Fase
Energia, fenómenos térmicos e radiação
#222 - Exame Física e Química A - 2020, 1ª Fase
Forças e movimentos
#791 - Exame Física e Química A - 2014, 1ª Fase
Ondas eletromagnéticas
#3.1 - Exame Física e Química A - 2024, 2ª Fase
Eletromagnetismo
#2.2 - Exame Física e Química A - 2023, 1ª Fase
Ondas eletromagnéticas
#4 - Exame Física e Química A - 2023, 1ª Fase
Energia, fenómenos térmicos e radiação
#522 - Exame Física e Química A - 2016, 1ª Fase
Eletromagnetismo
#5.1 - Exame Física e Química A - 2021, Época Especial
Energia, fenómenos térmicos e radiação
#252 - Exame Física e Química A - 2020, 1ª Fase
Interações e seus efeitos
#258 - Exame Física e Química A - 2020, 1ª Fase
Energia e fenómenos elétricos
#5.2 - Exame Física e Química A - 2023, Época Especial
Tempo, posição, velocidade e aceleração
#556 - Exame Física e Química A - 2016, 1ª Fase
Energia, fenómenos térmicos e radiação
#795 - Exame Física e Química A - 2014, 1ª Fase
Energia e movimentos
#758 - Exame Física e Química A - 2015, 1ª Fase
Forças e movimentos
#7.3 - Exame Física e Química A - 2022, 1ª Fase
Energia e fenómenos elétricos
#356 - Exame Física e Química A - 2019, 1ª Fase
Energia e movimentos
#634 - Exame Física e Química A - 2014, 1ª Fase
Eletromagnetismo
#3.1 - Exame Física e Química A - 2023, 2ª Fase
Ondas eletromagnéticas
#227 - Exame Física e Química A - 2020, 1ª Fase
Energia, fenómenos térmicos e radiação
#790 - Exame Física e Química A - 2014, 1ª Fase
Energia, fenómenos térmicos e radiação
#410 - Exame Física e Química A - 2018, 1ª Fase
Energia, fenómenos térmicos e radiação
#411 - Exame Física e Química A - 2018, 1ª Fase
Eletromagnetismo
#5.4 - Exame Física e Química A - 2022, 1ª Fase
Sinais e ondas
#493 - Exame Física e Química A - 2017, 1ª Fase
Forças e movimentos
#7.2 - Exame Física e Química A - 2024, Época Especial
Forças e movimentos
#439 - Exame Física e Química A - 2018, 1ª Fase
Energia, fenómenos térmicos e radiação
#10.2.1 - Exame Física e Química A - 2023, 2ª Fase
Energia, fenómenos térmicos e radiação
#7.1 - Exame Física e Química A - 2024, 1ª Fase
Forças e movimentos
#317 - Exame Física e Química A - 2019, 1ª Fase
Interações e seus efeitos
#722 - Exame Física e Química A - 2016, 1ª Fase
Forças e movimentos
#219 - Exame Física e Química A - 2020, 1ª Fase
Forças e movimentos
#9.1 - Exame Física e Química A - 2023, 2ª Fase
Forças e movimentos
#353 - Exame Física e Química A - 2019, 1ª Fase
Tempo, posição, velocidade e aceleração
#347 - Exame Física e Química A - 2019, 1ª Fase
Sinais e ondas
#488 - Exame Física e Química A - 2017, 1ª Fase
Energia e movimentos
#713 - Exame Física e Química A - 2017, 1ª Fase
Forças e movimentos
#277 - Exame Física e Química A - 2020, 1ª Fase
Energia, fenómenos térmicos e radiação
#585 - Exame Física e Química A - 2015, 1ª Fase
Sinais e ondas
#409 - Exame Física e Química A - 2018, 1ª Fase
Energia, fenómenos térmicos e radiação
#9.2.2 - Exame Física e Química A - 2023, Época Especial
Forças e movimentos
#672 - Exame Física e Química A - 2014, 1ª Fase
Ondas eletromagnéticas
#300 - Exame Física e Química A - 2019, 1ª Fase
Energia, fenómenos térmicos e radiação
#6.2 - Exame Física e Química A - 2021, 2ª Fase
Interações e seus efeitos
#789 - Exame Física e Química A - 2014, 1ª Fase
Energia, fenómenos térmicos e radiação
#401 - Exame Física e Química A - 2018, 1ª Fase
Forças e movimentos
#4.4 - Exame Física e Química A - 2024, 2ª Fase
Forças e movimentos
#10.2.2 - Exame Física e Química A - 2023, 2ª Fase
Energia, fenómenos térmicos e radiação
#9.2 - Exame Física e Química A - 2023, 2ª Fase
Energia e movimentos
#319 - Exame Física e Química A - 2019, 1ª Fase
Forças e movimentos
#496 - Exame Física e Química A - 2017, 1ª Fase
Energia, fenómenos térmicos e radiação
#259 - Exame Física e Química A - 2020, 1ª Fase
Sinais e ondas
#378 - Exame Física e Química A - 2018, 1ª Fase
Energia e movimentos
#2.1 - Exame Física e Química A - 2024, 1ª Fase
Energia, fenómenos térmicos e radiação
#7.3 - Exame Física e Química A - 2024, 1ª Fase
Energia e movimentos
#554 - Exame Física e Química A - 2016, 1ª Fase
Energia, fenómenos térmicos e radiação
#725 - Exame Física e Química A - 2016, 1ª Fase
Energia e movimentos
#1.2 - Exame Física e Química A - 2024, 2ª Fase
Energia, fenómenos térmicos e radiação
#3.1 - Exame Física e Química A - 2022, Época Especial
Tempo, posição, velocidade e aceleração
#491 - Exame Física e Química A - 2017, 1ª Fase
Interações e seus efeitos
#583 - Exame Física e Química A - 2015, 1ª Fase
Energia e movimentos
#645 - Exame Física e Química A - 2014, 1ª Fase
Forças e movimentos
#334 - Exame Física e Química A - 2019, 1ª Fase
Energia, fenómenos térmicos e radiação
#1.1 - Exame Física e Química A - 2022, 2ª Fase
Eletromagnetismo
#405 - Exame Física e Química A - 2018, 1ª Fase
Energia e movimentos
#5.2.1 - Exame Física e Química A - 2023, 2ª Fase
Energia e fenómenos elétricos
#499 - Exame Física e Química A - 2017, 1ª Fase
Ondas eletromagnéticas
#492 - Exame Física e Química A - 2017, 1ª Fase
Forças e movimentos
#297 - Exame Física e Química A - 2019, 1ª Fase
Sinais e ondas
#379 - Exame Física e Química A - 2018, 1ª Fase
Energia e movimentos
#666 - Exame Física e Química A - 2014, 1ª Fase
Forças e movimentos
#273 - Exame Física e Química A - 2020, 1ª Fase
Energia e movimentos
#626 - Exame Física e Química A - 2015, 1ª Fase
Energia e movimentos
#256 - Exame Física e Química A - 2020, 1ª Fase
Energia e movimentos
#260 - Exame Física e Química A - 2020, 1ª Fase
Ondas eletromagnéticas
#2.1 - Exame Física e Química A - 2021, Época Especial
Forças e movimentos
#770 - Exame Física e Química A - 2015, 1ª Fase
Energia e movimentos
#375 - Exame Física e Química A - 2018, 1ª Fase
Energia, fenómenos térmicos e radiação
#403 - Exame Física e Química A - 2018, 1ª Fase
Forças e movimentos
#272 - Exame Física e Química A - 2020, 1ª Fase
Forças e movimentos
#799 - Exame Física e Química A - 2014, 1ª Fase
Interações e seus efeitos
#380 - Exame Física e Química A - 2018, 1ª Fase
Interações e seus efeitos
#1.1 - Exame Física e Química A - 2021, 1ª Fase
Energia, fenómenos térmicos e radiação
#438 - Exame Física e Química A - 2018, 1ª Fase
Energia, fenómenos térmicos e radiação
#440 - Exame Física e Química A - 2018, 1ª Fase
Sinais e ondas
#665 - Exame Física e Química A - 2014, 1ª Fase
Forças e movimentos
#664 - Exame Física e Química A - 2014, 1ª Fase
Energia e movimentos
#280 - Exame Física e Química A - 2020, 1ª Fase
Sinais e ondas
#3.2 - Exame Física e Química A - 2022, Época Especial
Forças e movimentos
#3.2 - Exame Física e Química A - 2021, Época Especial
Interações e seus efeitos
#1.3 - Exame Física e Química A - 2024, 2ª Fase
Energia e fenómenos elétricos
#414 - Exame Física e Química A - 2018, 1ª Fase
Eletromagnetismo
#635 - Exame Física e Química A - 2014, 1ª Fase
Eletromagnetismo
#644 - Exame Física e Química A - 2014, 1ª Fase
Forças e movimentos
#633 - Exame Física e Química A - 2014, 1ª Fase
Eletromagnetismo
#4.1 - Exame Física e Química A - 2024, Época Especial
Energia e movimentos
#9.3 - Exame Física e Química A - 2024, Época Especial
Ondas eletromagnéticas
#269 - Exame Física e Química A - 2020, 1ª Fase
Interações e seus efeitos
#437 - Exame Física e Química A - 2018, 1ª Fase
Energia, fenómenos térmicos e radiação
#429 - Exame Física e Química A - 2018, 1ª Fase
Tempo, posição, velocidade e aceleração
#296 - Exame Física e Química A - 2019, 1ª Fase
Sinais e ondas
#337 - Exame Física e Química A - 2019, 1ª Fase
Ondas eletromagnéticas
#335 - Exame Física e Química A - 2019, 1ª Fase
Eletromagnetismo
#3.1 - Exame Física e Química A - 2021, Época Especial
Energia e movimentos
#473 - Exame Física e Química A - 2017, 1ª Fase
Ondas eletromagnéticas
#464 - Exame Física e Química A - 2017, 1ª Fase
Energia, fenómenos térmicos e radiação
#465 - Exame Física e Química A - 2017, 1ª Fase
Energia, fenómenos térmicos e radiação
#470 - Exame Física e Química A - 2017, 1ª Fase
Energia e movimentos
#469 - Exame Física e Química A - 2017, 1ª Fase
Energia e movimentos
#752 - Exame Física e Química A - 2015, 1ª Fase
Ondas eletromagnéticas
#663 - Exame Física e Química A - 2014, 1ª Fase
Energia e movimentos
#661 - Exame Física e Química A - 2014, 1ª Fase
Interações e seus efeitos
#668 - Exame Física e Química A - 2014, 1ª Fase
Energia, fenómenos térmicos e radiação
#667 - Exame Física e Química A - 2014, 1ª Fase
Forças e movimentos
#696 - Exame Física e Química A - 2017, 1ª Fase
Energia, fenómenos térmicos e radiação
#715 - Exame Física e Química A - 2017, 1ª Fase
Forças e movimentos
#226 - Exame Física e Química A - 2020, 1ª Fase
Energia, fenómenos térmicos e radiação
#271 - Exame Física e Química A - 2020, 1ª Fase
Forças e movimentos
#295 - Exame Física e Química A - 2019, 1ª Fase
Sinais e ondas
#570 - Exame Física e Química A - 2016, 1ª Fase
Ondas eletromagnéticas
#274 - Exame Física e Química A - 2020, 1ª Fase
Energia, fenómenos térmicos e radiação
#230 - Exame Física e Química A - 2020, 1ª Fase
Eletromagnetismo
#261 - Exame Física e Química A - 2020, 1ª Fase
Forças e movimentos
#253 - Exame Física e Química A - 2020, 1ª Fase
Energia e movimentos
#251 - Exame Física e Química A - 2020, 1ª Fase
Energia, fenómenos térmicos e radiação
#254 - Exame Física e Química A - 2020, 1ª Fase
Energia e movimentos
#250 - Exame Física e Química A - 2020, 1ª Fase
Energia, fenómenos térmicos e radiação
#5.1.1 - Exame Física e Química A - 2022, Época Especial
Energia e fenómenos elétricos
#5.1.2 - Exame Física e Química A - 2022, Época Especial
Ondas eletromagnéticas
#2.1 - Exame Física e Química A - 2022, Época Especial
Energia, fenómenos térmicos e radiação
#584 - Exame Física e Química A - 2015, 1ª Fase
Sinais e ondas
#578 - Exame Física e Química A - 2015, 1ª Fase
Forças e movimentos
#7.1 - Exame Física e Química A - 2021, Época Especial
Energia e fenómenos elétricos
#5.1 - Exame Física e Química A - 2021, 2ª Fase
Ondas eletromagnéticas
#794 - Exame Física e Química A - 2014, 1ª Fase
Forças e movimentos
#643 - Exame Física e Química A - 2014, 1ª Fase
Forças e movimentos
#1.2 - Exame Física e Química A - 2022, 1ª Fase
Forças e movimentos
#728 - Exame Física e Química A - 2016, 1ª Fase
Energia, fenómenos térmicos e radiação
#6.2 - Exame Física e Química A - 2024, Época Especial
Eletromagnetismo
#4.3 - Exame Física e Química A - 2024, Época Especial
Energia e fenómenos elétricos
#340 - Exame Física e Química A - 2019, 1ª Fase
Forças e movimentos
#772 - Exame Física e Química A - 2015, 1ª Fase
Eletromagnetismo
#2.2 - Exame Física e Química A - 2021, Época Especial
Forças e movimentos
#466 - Exame Física e Química A - 2017, 1ª Fase
Sinais e ondas
#519 - Exame Física e Química A - 2016, 1ª Fase
Forças e movimentos
#788 - Exame Física e Química A - 2014, 1ª Fase
Energia, fenómenos térmicos e radiação
#476 - Exame Física e Química A - 2017, 1ª Fase
Interações e seus efeitos
#479 - Exame Física e Química A - 2017, 1ª Fase
Interações e seus efeitos
#471 - Exame Física e Química A - 2017, 1ª Fase
Energia e movimentos
#769 - Exame Física e Química A - 2015, 1ª Fase
Energia e movimentos
#771 - Exame Física e Química A - 2015, 1ª Fase
Eletromagnetismo
#377 - Exame Física e Química A - 2018, 1ª Fase
Interações e seus efeitos
#373 - Exame Física e Química A - 2018, 1ª Fase
Energia, fenómenos térmicos e radiação
#623 - Exame Física e Química A - 2015, 1ª Fase
Energia, fenómenos térmicos e radiação
#573 - Exame Física e Química A - 2016, 1ª Fase
Ondas eletromagnéticas
#572 - Exame Física e Química A - 2016, 1ª Fase
Ondas eletromagnéticas
#5.1 - Exame Física e Química A - 2023, 1ª Fase
Energia e movimentos
#407 - Exame Física e Química A - 2018, 1ª Fase
Energia e movimentos
#5.2.1 - Exame Física e Química A - 2023, 1ª Fase
Forças e movimentos
#6.3 - Exame Física e Química A - 2022, 2ª Fase
Interações e seus efeitos
#732 - Exame Física e Química A - 2016, 1ª Fase
Ondas eletromagnéticas
#369 - Exame Física e Química A - 2019, 1ª Fase
Energia, fenómenos térmicos e radiação
#516 - Exame Física e Química A - 2016, 1ª Fase
Tempo, posição, velocidade e aceleração
#350 - Exame Física e Química A - 2019, 1ª Fase
Energia, fenómenos térmicos e radiação
#5.1 - Exame Física e Química A - 2023, 2ª Fase
Tempo, posição, velocidade e aceleração
#9.3 - Exame Física e Química A - 2023, 2ª Fase
Energia, fenómenos térmicos e radiação
#495 - Exame Física e Química A - 2017, 1ª Fase
Energia, fenómenos térmicos e radiação
#6.1 - Exame Física e Química A - 2024, 1ª Fase
Energia e fenómenos elétricos
#604 - Exame Física e Química A - 2015, 1ª Fase
Tempo, posição, velocidade e aceleração
#605 - Exame Física e Química A - 2015, 1ª Fase
Eletromagnetismo
#628 - Exame Física e Química A - 2015, 1ª Fase
Forças e movimentos
#381 - Exame Física e Química A - 2018, 1ª Fase
Energia e movimentos
#4.3 - Exame Física e Química A - 2024, 2ª Fase
Tempo, posição, velocidade e aceleração
#564 - Exame Física e Química A - 2016, 1ª Fase
Energia e movimentos
#571 - Exame Física e Química A - 2016, 1ª Fase
Ondas eletromagnéticas
#404 - Exame Física e Química A - 2018, 1ª Fase
Energia e movimentos
#412 - Exame Física e Química A - 2018, 1ª Fase
Eletromagnetismo
#413 - Exame Física e Química A - 2018, 1ª Fase
Eletromagnetismo
#5.4.2 - Exame Física e Química A - 2023, 1ª Fase
Energia e fenómenos elétricos
#6.1 - Exame Física e Química A - 2022, 1ª Fase
Forças e movimentos
#7.1 - Exame Física e Química A - 2022, 1ª Fase
Energia e fenómenos elétricos
#731 - Exame Física e Química A - 2016, 1ª Fase
Ondas eletromagnéticas
#724 - Exame Física e Química A - 2016, 1ª Fase
Energia e movimentos
#726 - Exame Física e Química A - 2016, 1ª Fase
Energia e movimentos
#348 - Exame Física e Química A - 2019, 1ª Fase
Sinais e ondas
#354 - Exame Física e Química A - 2019, 1ª Fase
Energia e movimentos
#357 - Exame Física e Química A - 2019, 1ª Fase
Forças e movimentos
#4 - Exame Física e Química A - 2023, 2ª Fase
Forças e movimentos
#625 - Exame Física e Química A - 2015, 1ª Fase
Energia e movimentos
#631 - Exame Física e Química A - 2015, 1ª Fase
Forças e movimentos
#603 - Exame Física e Química A - 2015, 1ª Fase
Ondas eletromagnéticas
#4.3 - Exame Física e Química A - 2022, Época Especial
Forças e movimentos
#768 - Exame Física e Química A - 2015, 1ª Fase
Energia e movimentos
#1.3.2 - Exame Física e Química A - 2022, 2ª Fase
Energia, fenómenos térmicos e radiação
#257 - Exame Física e Química A - 2020, 1ª Fase
Eletromagnetismo
#797 - Exame Física e Química A - 2014, 1ª Fase
Energia e movimentos
#773 - Exame Física e Química A - 2015, 1ª Fase
Energia, fenómenos térmicos e radiação
#270 - Exame Física e Química A - 2020, 1ª Fase
Energia e movimentos
#759 - Exame Física e Química A - 2015, 1ª Fase
Energia, fenómenos térmicos e radiação
#385 - Exame Física e Química A - 2018, 1ª Fase
Ondas eletromagnéticas
#566 - Exame Física e Química A - 2016, 1ª Fase
Interações e seus efeitos
#565 - Exame Física e Química A - 2016, 1ª Fase
Energia e movimentos
#408 - Exame Física e Química A - 2018, 1ª Fase
Energia, fenómenos térmicos e radiação
#5.4.1 - Exame Física e Química A - 2023, 1ª Fase
Energia e fenómenos elétricos
#2.2 - Exame Física e Química A - 2022, 2ª Fase
Forças e movimentos
#1.1.1 - Exame Física e Química A - 2022, 1ª Fase
Tempo, posição, velocidade e aceleração
#579 - Exame Física e Química A - 2015, 1ª Fase
Forças e movimentos
Dificuldade: fácil
Mostrar Enunciado do Grupo
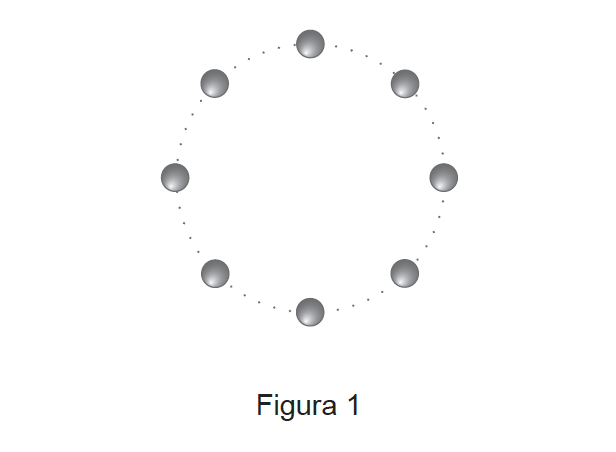
Uma bola, atada a uma corda, descreve trajetórias circulares num mesmo plano horizontal.
Considere que a bola pode ser representada pelo seu centro de massa (modelo da partícula material).
Questão:
Na Figura 1, está representada uma imagem estroboscópica de um movimento da bola, no qual a trajetória descrita pela bola é uma circunferência de raio $30 \mathrm{~cm}$. Nessa imagem estroboscópica, as posições da bola foram registadas a intervalos de tempo de $4,0 \times 10^{-2} \mathrm{~s}$.
Determine o módulo da aceleração da bola no movimento considerado.
Apresente todas as etapas de resolução.
Comentários
Neste momento, não há comentários para este exercício.
Para comentar, por favor inicia sessão ou cria uma conta.
