Mestre Panda

Dificuldade: fácil

Mostrar Enunciado do Grupo

Um automóvel encontrava-se estacionado no cimo de uma rampa, como se representa na Figura 1 (que não está à escala), quando, acidentalmente, se destravou. Deslizou ao longo da rampa, com aceleração constante, até colidir com um motociclo que se encontrava parado.

Considere que, no movimento considerado, a resultante das forças dissipativas que atuaram no automóvel não foi desprezável, e considere que o automóvel pode ser representado pelo seu centro de massa (modelo da partícula material).

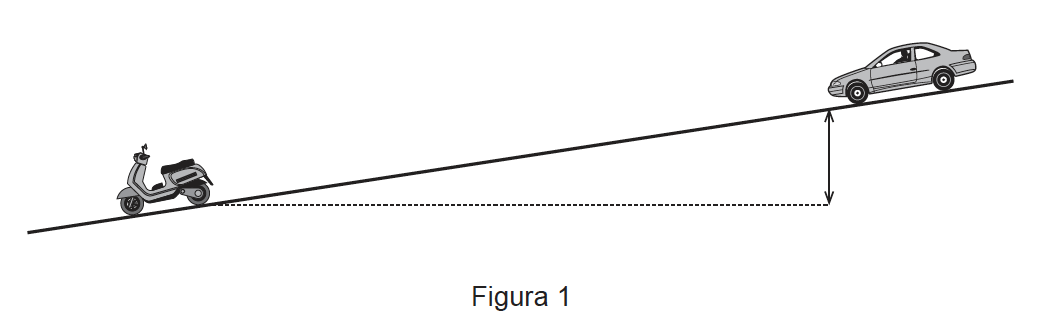
O automóvel, de massa $1,2 \times 10^{3} \mathrm{~kg}$, deslizou $80 \mathrm{~m}$ ao longo da rampa até colidir com o motociclo. A análise do acidente permitiu determinar que o módulo da velocidade do automóvel no instante da colisão era $7,5 \mathrm{~m} \mathrm{~s}^{-1}$.

Considere que o desnível entre as posições inicial e final do automóvel era 7,0 m.

Questão:

Determine o tempo que o automóvel demorou a percorrer aquela distância sobre a rampa, a partir de um esboço do gráfico do módulo da velocidade do automóvel em função do tempo (apresente esse esboço).

Mostre como chegou ao valor solicitado.

Fonte: Exame Física e Química A - 2020, 1ª Fase - Grupo Exercício 255

Resumos